Page describing on-going effort to clarify the calculation of roughness length in ORCHIDEE and investigate/solve the biais in bare soil evaporation
- Page describing on-going effort to clarify the calculation of roughness …
Testing roughness length for heat in LMDZOR
01-Sep-2015 by Fuxing WANG, Frederique CHERUY.
Background:
The roughness length for heat (z0h) is generally not identical to roughness length for momentum (z0m).
In LMDZOR, z0h = z0m. A short description of related code is (only in coupled mode): https://forge.ipsl.jussieu.fr/orchidee/attachment/wiki/DevelopmentActivities/CMIP6/DevelopmentsCMIP6/soil_physic/condveg_z0cdrag.pdf
Objective:
To test the sensitively of LMDZOR to z0h.
Simulations:
Two simulations (1-year) were done with LMDZOR after 20 years spin-up.
(1) CTL: z0h = z0m; ORCHIDEE-rev 2664, LMDZ-rev 2287; new soil vertical discretization and soil thermodynamics
(2) EXP: The same as CTL, but z0h = 0.1 * z0m.
Results:
Results are compared over different seasons (annual mean, JJA and DJF): https://forge.ipsl.jussieu.fr/orchidee/attachment/wiki/DevelopmentActivities/CMIP6/DevelopmentsCMIP6/soil_physic/z0mh_annual_jja_djf.pdf.
The left side in the figures is "CTL: z0h = z0m", the right side is the 'EXP-CTL' (except the last row which is the " EXP/CTL").
The Ts (temp_sol) increases over most regions. The maximum increase is over 0N-90N in JJA (1-2K), while it is over 30N-60S in DJF (0.5-1.5K).(Fig b)
The pattern of fluxsens is similar for different seasons. It increases over most regions (3 W/m2 for most regions).
The variation of fluxlat (+/- 6 W/m2 over most regions) and precipitation (+/-0.5mm/d over most regions) is less systematic than Ts and fluxsens.
Summary of ORCHIDEE DEV meeting on 6 Oct. 2015
Time: 6 Oct. 2015, 10H00-12H20
Place: Jussieu, Atrium room (big one), LSCE (through vdeo conference)
Participants: Philippe P., Agnes D., Frederique C., Nicolas V., Jan P., Pascal M., Ardalan T., Josefine G., Matthieu G., Adriana S., Anais B., Sonia A., Fuxing W., ...
The meeting includes four parts.
Link to all the presentations:
https://forge.ipsl.jussieu.fr/orchidee/wiki/GroupActivities/Meetings/Developer#a06102015-BaresoilevaporationBSEandroughnesslengthz0
Part 0: Introduction.
Philippe P. shortly summarized the current status in the ORCHDIEE trunk (e.g., the water balance problem, the new driver, the new thermal properties, ...)
Part 1 (around 1 hour): Four presentations by Agnes D., Ardalan T., Nicolas V., and Fuxing W.
(1). Agnes D. presented the bare soil evaporation (BSE) parameterization in ORCHIDEE 11.
BSE is overestimated in ORCHDIEE 11.
(2). Ardalan T. presented the varies tests by adding soil resistance in BSE.
Jan P. suggested to do test with different number of top soil layers.
(3). Nicolas V. presented the Su et al., 2001 in ORCHDIEE offline model.
Currently, the veget_max is used for calculating z0 over forest.
The objective is to parameterize z0 using dynamic vegetation (e.g., LAI).
z0 from 'Su' were tested over site scale, it improves the latent heat and sensible heat simulation.
(4). Fuxing W. presented the testing of z0 in LMDZOR coupled simulation.
In general, z0m is different from z0h. Four formulas were tested: z0h = z0m/10; z0h = z0m/100; S01 [Su et al., 2001, JAM]; CZ09 [Chen and Zhang, 2009, GRL];
--> T2m increases (LE decreases) with the decrease of z0h;
--> These modifications compensate part of CMIP6 T2m (underestimated) and LE (overestimated) bias.
T2m increases when d is considered in LMDZ and when von karman constant (=0.4) is used in ORCHIDEE-LMDZ.
Part 2: Discussions (around 1 hour).
(1) The treat of z0m and z0h in LMDZ and ORCHDIEE.
Jan P.: Theoretically, the ORCHIDEE should provide z0h (but not z0m) to LMDZ, ORCHIDEE does not need z0m.
ORCHIDEE uses z0h to calculate the heat/water flux.
LMDZ then calculate the z0m by considering the large scale orography effects.
Adriana S.:
Currently, LMDZ is using the z0 from ORCHIDEE as z0m, and z0h = z0m in PBL.
The orography effects have been considered in another way by Francois L., but z0m does not include it.
(Adriana S. is now working on the LMDZ dust transport modeling.)
Fuxing W.: The z0 over bare soil is 0.01m in ORC.
If the z0 in ORCHIDEE is z0h, according to the fact that the z0m > z0h for most surfaces (z0m =10* z0h for example).
The z0m over bare soil will become too large (0.1 m).
(2) The implementing Su et al. (2001) or other "z0h ≠ z0m" method in ORCHIDEE offline and LMDZOR:
Question by Pascal M.: how many parameters to calibrate in Su's formula ?
Fuxing W. : The parameter marked in red in the slide (of Su's equations) need to calibrated for different vegetation types.
e.g., c1, c2, c3, Cd, Ct, ...
Other points by Fuxing W.: Su's formula has not been fully evaluated on global scale.
Many GCMs use a factor to modify the z0m to obtain z0h. The factor varies with land surface types but constant over time.
Some models use kB-1 method to parameteriza z0h (kB-1 = ln(z0m/z0h)).
Question by Jan: How the z0 over different land surfaces is considered in one model grid when testing Su's method ? Nicolas V.: There are two fractions in Su's formula: one for bare soil, another for vegetated surface. The grid mean value is obtained by weighting z0 over different surfaces. The same parameter is used over different PFT's.
Frederique C.: Some additional points about the tests done with LMDZ6-ORC and the bias.
--Eventhough the z0h=z0m/10 or the Su tests seem to go in the right direction, the correction they can bring are small with respect to the cold bias in the present simulations of LMdZ6/ORC11.
--the geographical patterns of the corrections do not match the actual patterns of the bias.
--The z0h=z0m/10 goes in the right direction when Fuxing assumes that it is z0m which is given by orchidee to LMDZ.
--The biais could be due to the PBL parameterization as well ( very cold biais over Groenland as well, which is not sensitive to z0) [ need to detailed analysis, tbd]
--The origin of the bias can be very different on dry regions such as desert and high latitudes.
--My understanding of the orography impact: The impact of the orography is not included in the cdragm, but the orography impacts the wind at the first atmospheric level which in turn impacts the exchange coefficient
--According to work of B. Marticorena and Catherine Prigent (at least over Sahara and Sahel), the values of z0 for bare soil in Orchidee are much higher than observations.
--In winter, we identified a cold bias with ORC11 and not with ORC2 when we evaluated LMDZ (new-physique of CMIP5) over SIRTA. This bias has been related to an excess of latent heat flux.
(3) zero plane displacement (d).
Question by Agnes. D: Is the d used in ORCHIDEE ?
Jan P.: Yes. It is considered when calculating the drag.
Point added by Fuxing W. in this summary: and d is not used here ?
in condveg_z0cdrag:z0(:) = z0(:) + d_veg(:) * (ct_karman/LOG(ztmp(:)/MAX(height(:,jv)*z0_over_height,z0_bare)))**2
Part 3: Conclusion.
To proceed, we propose:
(1) to correct von karman constant in ORCHIDEE from 0.35 to 0.40. (Nicolas V. has tested it in ORCHDIEE offline mode, it is not sensitive.)
(2) There are lots of evidence show that the z0h and z0m should be different . We agree that to implement different z0h and z0m in LMDZOR.
(3) Jan P. : There are currently two subroutines in condveg.f90 to calculate the grid average z0 : condveg_z0logz and condveg_z0cdrag.
We should think a better way and keep only one method.
d0 needs to be transferred to LMDZ and used there. This is a big error which needs to be fixed.
(4) Frederique C. is curious to know the effects of bare soil scheme on surface meteorology at global scale.
(5) We also agreed to make a review of how z0s are calculated in both ORCHIDEE and LMDZ, highlighting the inconsistencies between the two models, the zones that remain unclear (like around topographic drag), and the order of magnitudes of the involved quantities (z0 mostly), since the goal is not only to change the calculations, but also to improve them, and for good reasons.
Additional results by Jan Polcher
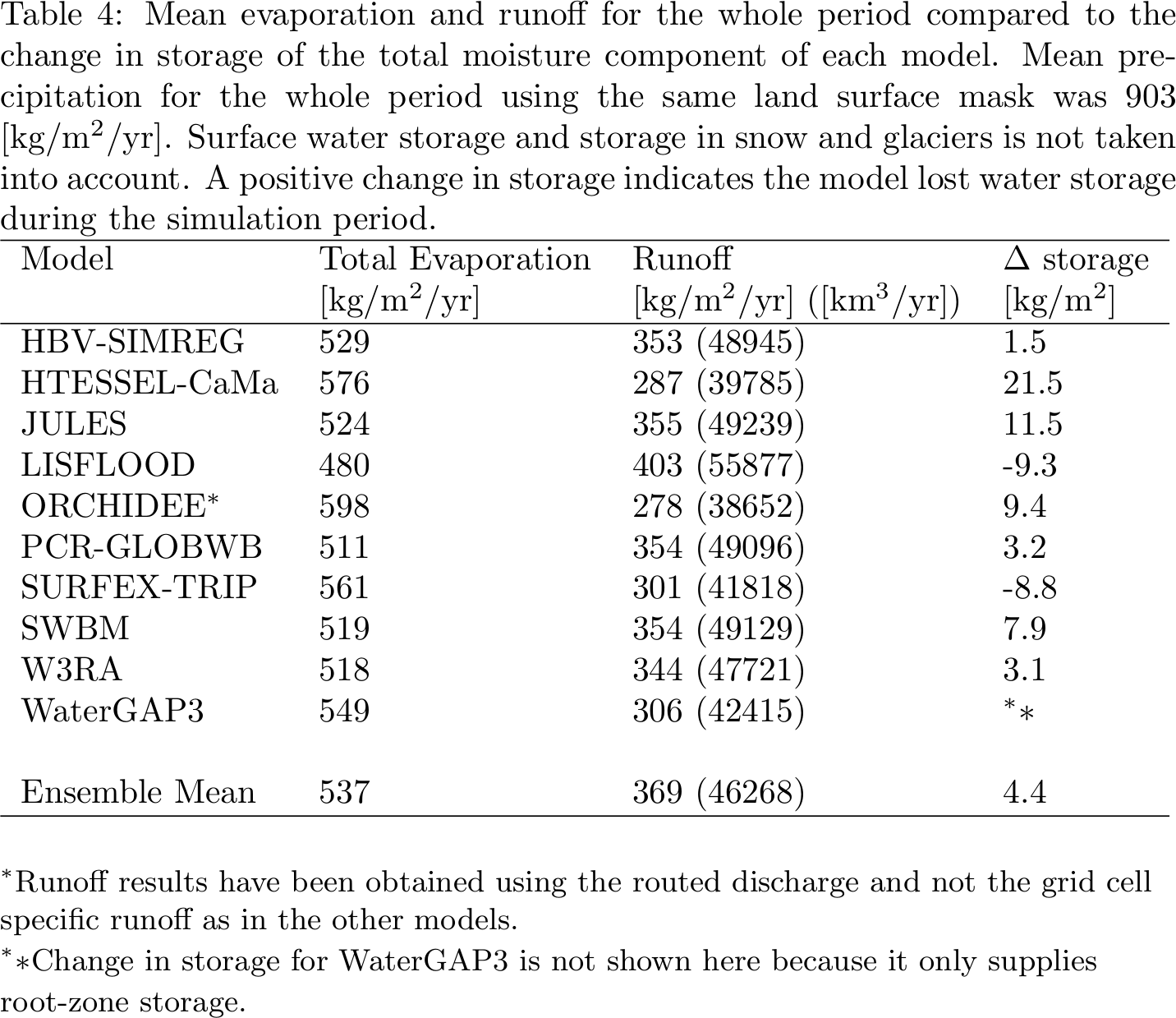
Within the Earth2Observe project a paper on the Tier 1 simulations has been submitted by Schellekens et al.. it include the following table :
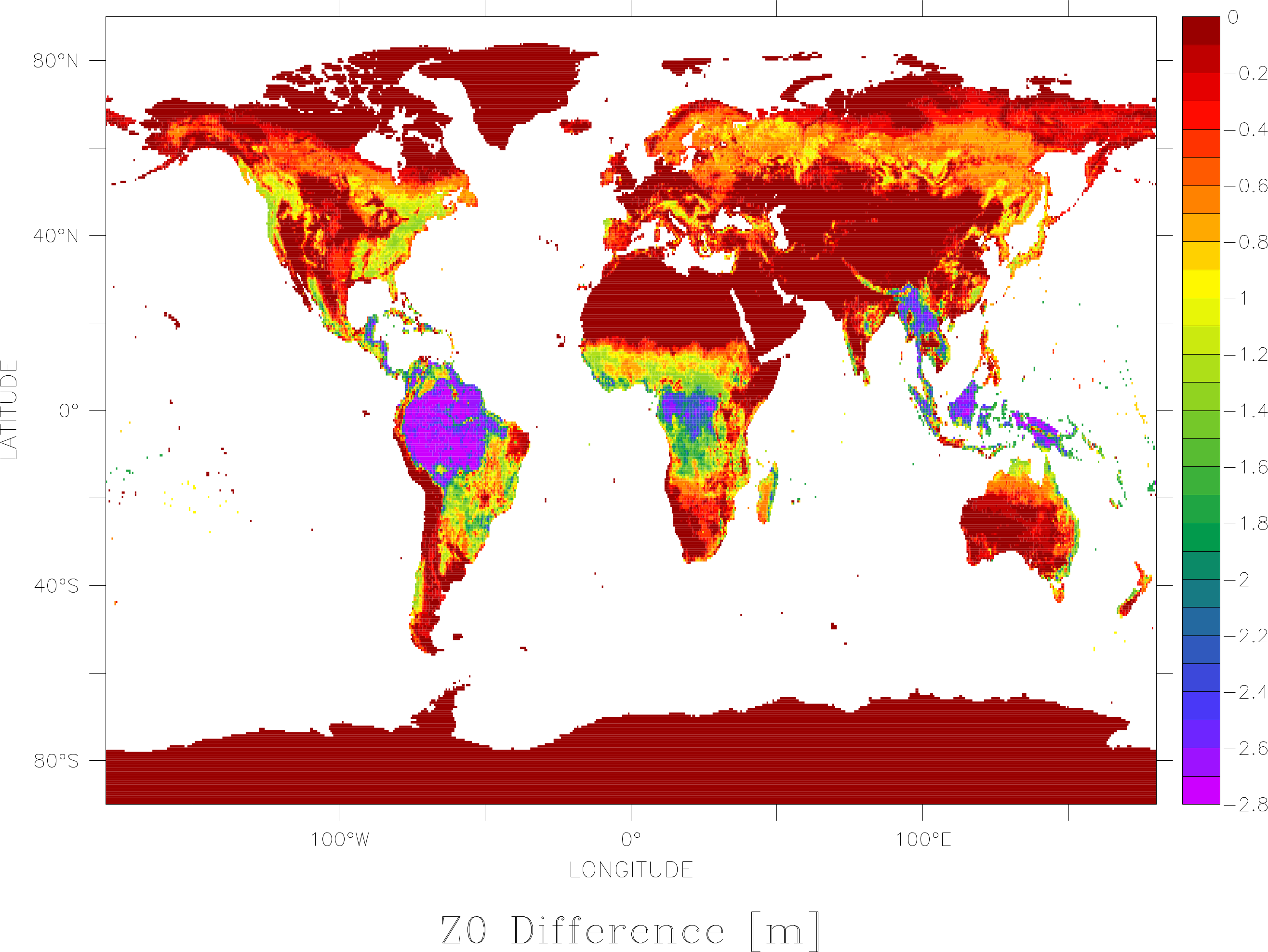
For this dataset it was the Trunk of July 2014 which was run but with the new driver. This meant a more accurate calculation of ETP from the WFDEI_CRU forcing. One immediately notes that evaporation is too high in ORCHIDEE and thus sets us apart from the other models. In order to test how much this is the result of years of accepting too high turbulence in order to compensate for too low ETPs produced the old driver, I re-ran the same code but dividing z0 by 10. The simulation is not yet finished so only the 90s are analysed.
The change in z0 is pictured below :
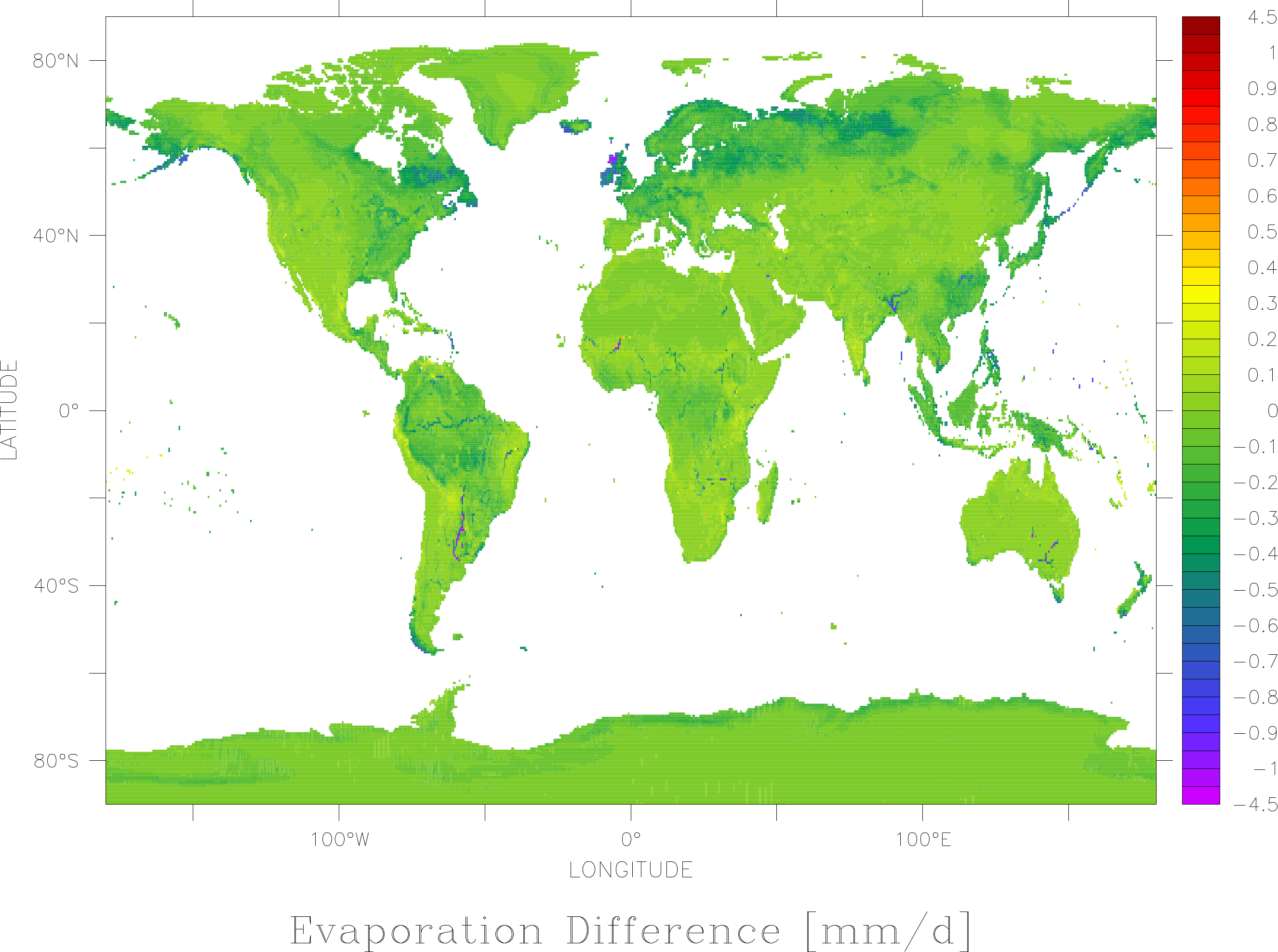
This modification leads to a weak but significant reduction of evaporation as pictures below :
Globally this translate into a reduction of evaporation of about 3.9%.
The analysis is performed over 34 WFDEI_CRU forcing years (1979-2012). We can apply this reduction to the mean ORCHIDEE number of 598 kg/m²/y and obtain 574 kg/m²/y. With this reduction, ORCHIDEE is still in the higher evaporating models but very close to HTESSEL and SURFEX.
This suggests to me that indeed we have been using Z0h=Z0m for years as a compensation for errors in the forcing. This is corroborated by analysis of the water cycle of the Mediterranean basin where ORCHIDEE systematically shows too much water in the rivers and thus too little evaporation. Choosing lower Z0h values in ORCHIDEE will allow to differentiate Z0m and Z0h in LMDZ, lowers evaporation and probably prepare us for a more complete parametrisation for estimating Z0h, like the one proposed by Su et al.
Results added on 12 Jan. 2015 by Fuxing WANG
- Regarding the question of the u* in SU's formula, sensitivity tests were done with LMDZOR (nudged):
(1) u* = [ c1 - c2 * exp(-c3 * cdrag_foliage * lai(:,jv)) ] * wind; (2) u* from lmdz.
The simulations are:
SU01Z0MH1: replace z0m and z0h by SU formula, u* by (1) method
SU01Z0MH2: same as SU01Z0MH1, but u* by (2) method
Results are shown in fig. z0mh_s01_mh_january.pdf
https://forge.ipsl.jussieu.fr/orchidee/attachment/wiki/DevelopmentActivities/CMIP6/DevelopmentsCMIP6/zo_evaporation/z0mh_s01_mh_january.pdf
The impacts of using different u* on temp_sol can be as large as 1-2K for vegetated area.
- The results by using SU formula with cdrag (neutral) corrected:
https://forge.ipsl.jussieu.fr/orchidee/attachment/wiki/DevelopmentActivities/CMIP6/DevelopmentsCMIP6/zo_evaporation/z0mh_SU.pdf
The model is LMDZ(NPv3.2)+ORCHIDEE(CWRR). It is 1-year nudged simulation after spinup.
In the figure, CTL means simulation using trunk. SU means simulation by changing z0m and z0h to SU's formula (same as Nicolas V. did).
The Ts increases by ~0.5K for most regions with the maximum increases being 1-1.5 K (JJA over desert).
The latent heat flux decreases by ~ 3-6 W/m2 for most regions.
Summary of the tests performed on z0 formula for reducing bare soil evaporation (N. Vuichard)
Context
Since the update of the 11-layer hydrological scheme into the trunk of ORCHIDEE in 2012, a strong positive bias on latent heat flux has been diagnosed with the 11-layer scheme at winter time for deciduous species compared to observations and compared to the 2-layer scheme. The figure below shows how the seasonal variations of the latent heat flux simulated with the 2-layer scheme and the 11-layer scheme compare to observations for different PFTs:
 |  |  |  |  |  |  | 
|
This overestimation of the latent flux when there is no contribution of transpiration but only bare soil evaporation is not observed over the cropland sites when the soil is bare.
The Su formulation
Consequently, one searched for a process/formula embedded into ORCHIDEE parametrized differently for trees and herbaceous PFTs and that may impact on the latent heat flux Analysis of the code. This is the case of the formulation of the roughness length (z0 parameter). In ORCHIDEE, one assumes that the roughness length of the herbaceous PFTs varies with the LAI, while the roughness length of Trees PFT does not. See the block of code here in condveg: https://forge.ipsl.jussieu.fr/orchidee/browser/trunk/ORCHIDEE/src_sechiba/condveg.f90?rev=2425#L1526
Some authors have proposed formulations of z0 which vary with the LAI as it is roughly done for herbaceous PFTs into ORCHIDEE. For instance, Su et al. (2001) developed such formulation which has been used and tested recently at fluxnet sites by Ershadi et al. (2015). The formulation of Su et al., 2001 has been implemented into ORCHIDEE. Inclusion the Su formula for z0 leads to reduce/cancel the bias on latent heat flux at winter for deciduous forest (TeDBF pfts). Results obtained with this formulation are shown below:
 |  |  |  |  |  |  | 
|
Here below is the mean seasonal fluxes averaged for all the sites per Biome (=PFT): in black are the observations, in green the standard ORCHIDEE and in red, the version with the formula of Su et al. (2001).
The "z0h=z0m/10" formulation
In the formulation of Su and many others, one distinguishes for the roughness length for heat (z0h) and for momentum (z0m). Fuxing has studied in coupled mode how accounting for both z0m and z0h in the formulation of the drag coefficient impacts on the surface fluxes and properties (temperature). Here we look at the impact on force in-situ simulations of accounting for the formula where z0h=z0m/10.
 |  |  |  |  |  |  | 
|
Here below is the mean seasonal fluxes averaged for all the sites per Biome (=PFT): in black are the observations, in green the standard ORCHIDEE and in red, the version with the formula "z0h=z0m/10".
Global off-line simulations
Global simulations with the 2 formulations have been performed. Synthesis of these 2 simulations is available: for the Su formulation (compared to the ctrl (=standard ORCHIDEE): http://vesg.ipsl.upmc.fr/thredds/fileServer/work/p529vui/OL2/DEVT/Eval-ORCHIDEE/Roughness/Forced_Global/3202/ATLAS_OBS_RDYN3202.su/index.html for the z0h formulation (compared to the ctrl) : http://vesg.ipsl.upmc.fr/thredds/fileServer/work/p529vui/OL2/DEVT/Eval-ORCHIDEE/Roughness/Forced_Global/r3202/ATLAS_OBS_RDYN3202.rz0h/index.html
Here below are few diagnostics specificly for the latent heat flux for the Su formulation:
 |  | 
|
And here the same diagnostics for the "z0h=z0m/10" formulation
 |  | 
|
Impact of the Su formulation on the Sensible Heat flux is significant in the global simulations while this was not the case in the in-situ simulations (see below). This might be related to the average of z0h and z0m over the different PFT fractions within each grid cell.
 |  | 
|
Comment on the averaging of z0 over tiles (N. Vuichard, 21/03/2016)
When we define the mean z0 by averaging the drag coefficient (cd), one uses the following relationship:
cd=(von_karman*LN(zref/z0m))*(von_karman*LN(zref/z0h))
When z0m and z0h are the same, it is easy to get a mean z0 from the mean cd by using the inverse relationship:
mean_z0=von_karman/EXP(zref/SQRT(cdmean))
where cdmean=SUM(veget_maxi*cdi) where i are the different tiles.
With different values for z0m and z0h, it is a bit more complicated.
When Fuxing and I, we worked with the formula z0h=z0m/10, we still used the calculation of cd with a single z0 (z0m) to get the mean z0m over the grid cell (in condveg). And then we were assuming that z0h,mean=z0m,mean/10.
But with those values of z0m,mean and z0h,mean, the mean drag coefficient over the pixel is not correct:
(von_karman*LN(zref/z0m,mean))*(von_karman*LN(zref/z0h,mean)) != cdmean
When implementing the formulation of Su, I used two calculations of cd: one with only z0m to get the mean z0m over the grid cell, and one with only z0h to get the mean z0h. With these values of z0m,mean and z0h,mean, the value of the mean cd is well approximated. For formulas in which z0h is a fixed fraction of z0m, it is a better approximation than assuming that z0h,mean=z0m,mean/10.
The attached spreadsheet (averaging_z0) summarizes the results we get with these different ways of calculating the mean z0 over the grid cells.
Additional runs that have been done
In Forced mode at local scale (Fluxnet)
Rough-Su-r3309-extcoeff: Comparison of version r3309 with the extinction coefficient to 1 (for defining the bare soil fraction) VS r3309 with the standard value of ext_coeff to 0.5
In Forced mode at global scale
3013: First test global simulation
3202: Main modifications compared to 3013 are related to revisions: r3065, r3081, r3084, r3197, r3199, r3202
3259: No main change, only r3259
3309: Modification are related to r3302, r3309.
3469: Main changes are related to r3422, r3436, r3456
In Coupled mode at global scale
Diagnostics can been found here: r3332
Attachments (11)
-
Table3.png
(230.1 KB) -
added by jpolcher 9 years ago.
Table 3 of Schellekens et al.
-
Evap_Diff.png
(568.0 KB) -
added by jpolcher 9 years ago.
Evaporation Difference over full period (1979-2012)
-
Z0_Diff.png
(536.4 KB) -
added by jpolcher 9 years ago.
Difference map for Z0
-
Table3_B.png
(230.1 KB) -
added by jpolcher 9 years ago.
Revised version of the Schellekens et al. paper
-
Z0_Diff_B.png
(536.4 KB) -
added by jpolcher 9 years ago.
Z0 Differences over the full period of simulation.
-
Evap_Diff_B.png
(568.0 KB) -
added by jpolcher 9 years ago.
Evaporation changes following the Z0/10 change for the period 1979-2012.
- z0mh_SU.pdf (2.8 MB) - added by fwang 8 years ago.
- z0mh_s01_mh_january.pdf (2.4 MB) - added by fwang 8 years ago.
-
su_2001.pdf
(592.4 KB) -
added by nvuilsce 8 years ago.
Su_2001
-
ershadietal2015.pdf
(1.1 MB) -
added by nvuilsce 8 years ago.
Ershadi_2015
-
averaging_z0.xlsx
(33.2 KB) -
added by nvuilsce 8 years ago.
How to compute the mean z0 over grid cells